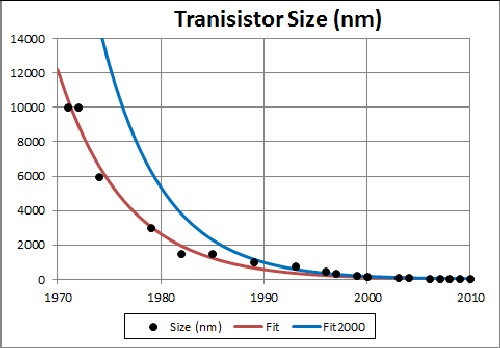
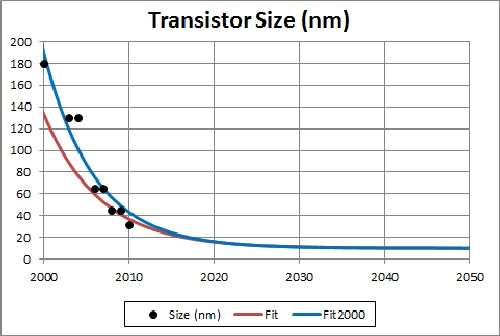
The Fit2000 curve is for restricting the fit to data from 2000 to the present.
L. David Roper
http://www.roperld.com/personal/roperldavid.htm
6 April, 2016
Computer processors are mostly made of silicon. In this article I fit the transistor size as a function of time with the hyperbolic tangent. The asymptotic limit is taken as 10 times the typical molecular size, 10 ångström (Å), or 100Å = 10 nm.
For references for the numbers given here see the Appendix 1.
See Appendix 2 for the fitting procedure.
The following show the fit curves and the data fitted:
The Fit2000 curve is for restricting the fit to data from 2000 to the present. |
 |
The transistor size will reach its 10 nm limit by about year 2030.
Of course, the "intelligence" of computers depends on program software, operating software, clock speed and how processors are organized, not just on the size of the transistors used. For example, the Intel i7-975-extreme machine that I am using has 4 cores and 8 threads.
I fit the following hyperbolic-tangent function to the data:
a + b exp[-(t-t0)/w],
where a = final steady value, b = strength of the decline, t0 is the time when the exponential = 1 and w is the "width" or time constant when t represents time, as is the case here.
This function assumes that the data being fitted goes from a high valuel through a transition with break point, t0, to a final steady value, a.l
Human Intelligence Evolution
L. David Roper interdisciplinary studies
L. David Roper, http://www.roperld.com/personal/roperldavid.htm
6 April, 2016