Electromagnetic Spectra of Light Bulbs

L. David Roper and Michael Rosenzweig

Introduction

Many homes are replacing incandescent light bulbs (IL: http://en.wikipedia.org/wiki/Incandescent_light_bulb) with compact fluorescent light bulbs (CFL: http://en.wikipedia.org/wiki/Compact_fluorescent) to save energy, because the CFL bulbs use about one-fourth of the energy that IL bulbs use to produce the same amount of light energy to which human eyes are sensitive (lumens: http://en.wikipedia.org/wiki/Lumens).

IL bulbs produce a continuous electromagnetic spectrum and CFL light bulbs produce a discrete spectrum. So, besides the amount of energy used to produce lumens, there is a consideration regarding the spectrum produced. Some people object to the spectral quality of CFL bulbs.

This article compares the spectra of IL and CFL bulbs with the solar spectrum at the Earth surface and with the sensitivity spectrum of the human eye and makes recommendations about matching the CFL spectra with the human-eye spectrum, the solar spectrum and the incandescent spectrum.

Matching CFL Spectrum to Other Spectra

There are at least three approaches that could be taken about the ideal frequencies that CFL bulbs should have:

1. Match the visual spectrum of the human eye.

2. Match the spectrum of IL bulbs.

3. Match the solar spectrum.

One could argue that #1. is the most important. However, one could also argue that modern humans are used to the IL spectrum, so perhaps it is what should be matched. But, one could also argue that humans evolved bathed in the solar spectrum, so perhaps it is what should be matched. The following graph shows these three spectra all normalized to 1. (Temperature = 3300 K for the IL bulb. Surface temperature of the Sun = 5800 K.)

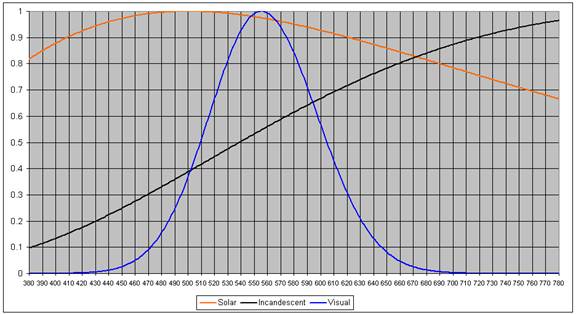
So, matching these three spectra are three completely different approaches, except for the middle frequencies.

General Electric has a web page that allows display of the spectra for its light bulbs:

http://www.gelighting.com/na/business_lighting/education_resources/learn_about_light/distribution_curves.htm

Consider the GE Daylight bulb: The spectrum is

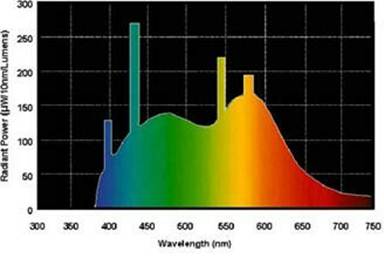
We created a reasonable model of this spectrum with six Gaussians, as shown in this graph:

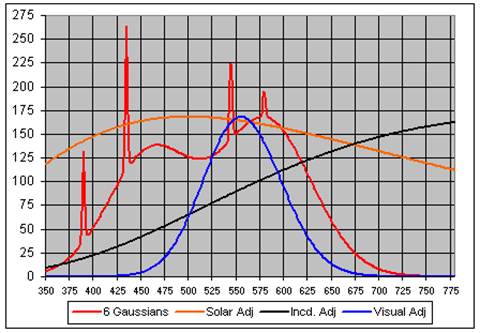
Also shown in the graph are the solar, incandescent and visual spectra normalized to the maximum of the two broad Gaussians. The correlation coefficients between the GE Daylight bulb and the (solar, incandescent and visual) spectra are (+0.906, -0.340 and +0.718).

Consider the GE Triphosphorus Fluorescent SP30 bulb: The spectrum is

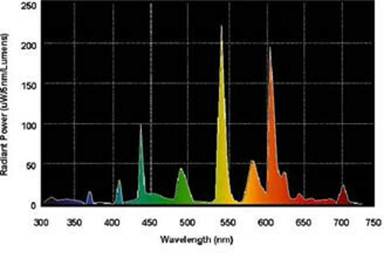
We created a reasonable model of this spectrum with eleven Gaussians, as shown in this graph:

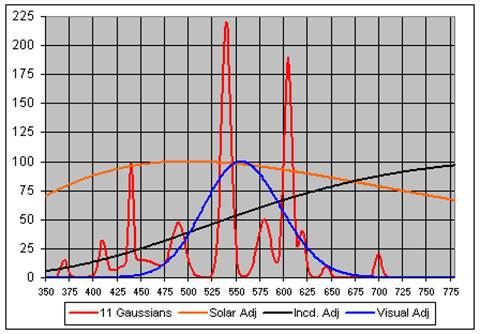
Also shown in the graph are the solar, incandescent and visual spectra normalized to approximately resemble the bulb’s spectrum. The correlation coefficients between the GE Daylight bulb and the (solar, incandescent and visual) spectra are (+0.376, -0.068 and +0.461).

Conclusions

Some conclusions that we can draw are:

· For the fluorescent bulb to better match the visual spectrum of the human eye, more or stronger lines are needed between 500 and 525 nm and between 550 and 600 nm..

· To better match the spectrum of IL bulbs, more or stronger lines are needed between 500 and 525 nm, 550 and 600, and above 625 nm.

· To better match the solar spectrum, lines are needed between 380 and 425 nm, 450 and 525 nm, 550 and 600, and above 625 nm.

http://www.roperld.com/science/electromagneticspectraoflightbulbs.pdf

Appendix

The solar spectrum and the incandescent spectrum are calculated from the Planck blackbody formula (http://en.wikipedia.org/wiki/Wien%27s_displacement_law) normalized to 1 at its peak:

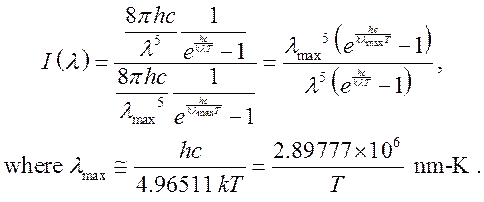
and

For the solar spectrum

The visual spectrum is represented by an asymmetric Gaussian:

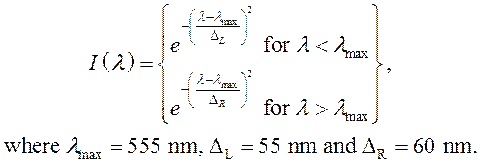
The spectrum for light bulbs is represented by a sum of N Gaussians:

L. David Roper
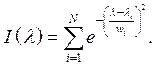
9 March 2007
http://www.roperld.com/personal/roperldavid.htm