L. David Roper
http://www.roperld.com/personal/roperldavid.htm
06-Apr-2016
In 1975 my colleague, Richard A. Arndt and I published a long article in the Journal of Theoretical Biology entitled Theory of Excitable Membranes I. A Simple Model for a Three-state Artificial Membrane. On this web page I summarize that article and expand it somewhat.
Here is the abstract for the article:
A simple physical-mathematical model is developed for an excitable artificial membrane consisting of a non-amphipathic lipid matrix spanned by protein channels having three conductance states. Although the model shows some of the features of squid axon data, the appropriate artificial membrane data are not available to these authors. A plea is made for collecting a complete set of data for simple symmetric and asymmetric excitable artificial membranes.
I display the figures and equations for the model taken from the article:

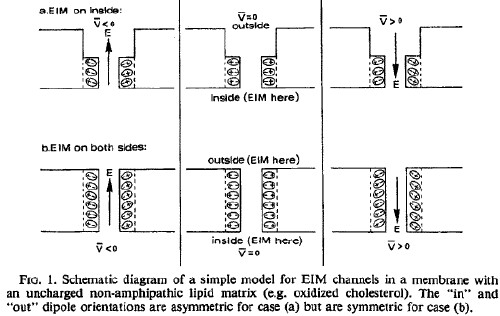
![]()
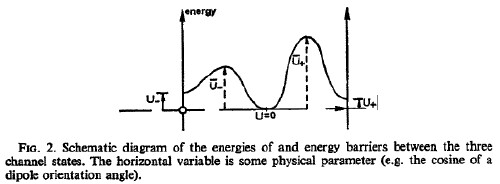
![]()
Added: An different equation that works equally well for the mobility is
![]() .
.
This expression has an extra term in the numerator and an extra term in the denominator compared to Eq. 2, both of which are very small (~10-18) for physically reasonable values of the parameters.
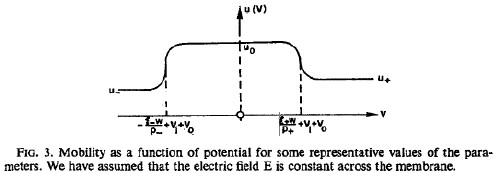
The time-dependent mobility is
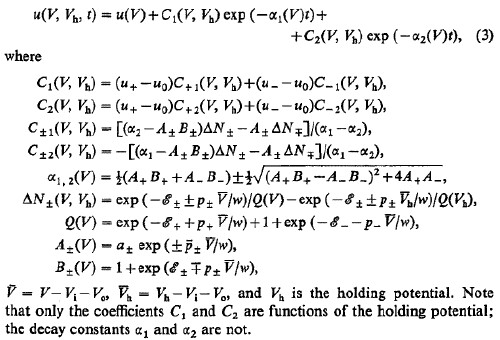
It is assumed that the electric field across the membrane is constant; then the steady-state current is
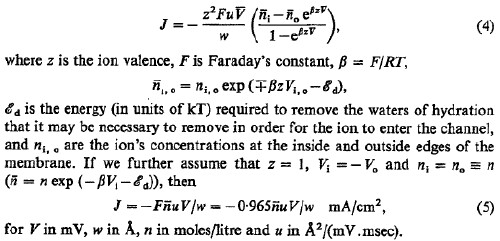
The following graphs show the mobility and current density for physically reasonable values of the parameters:
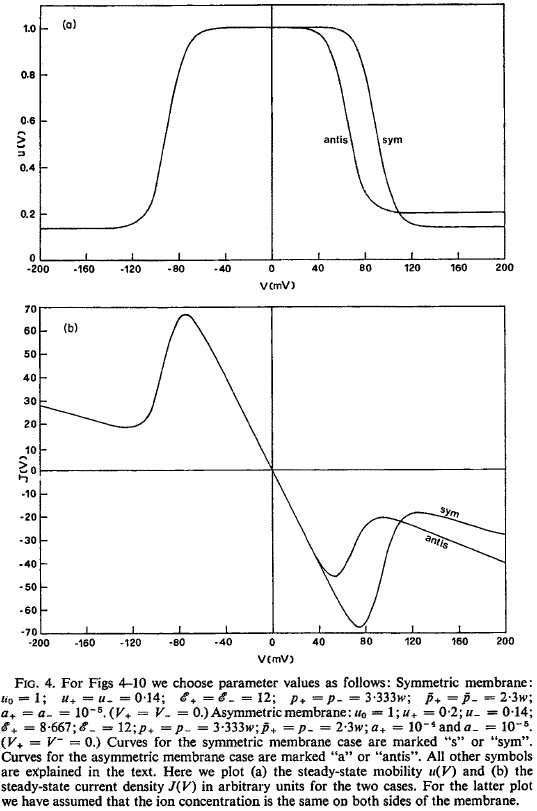
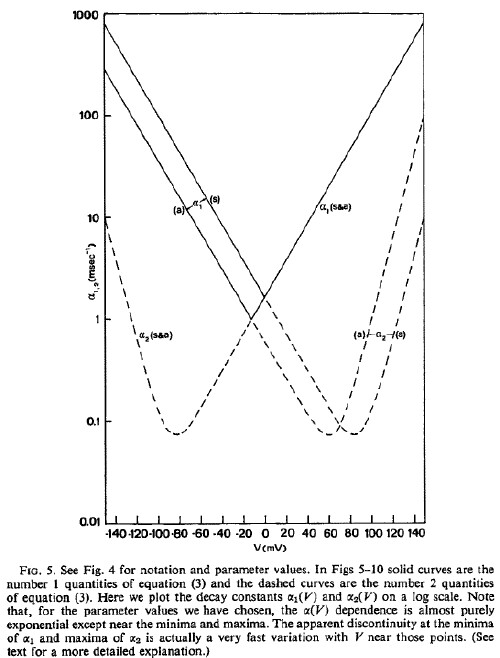
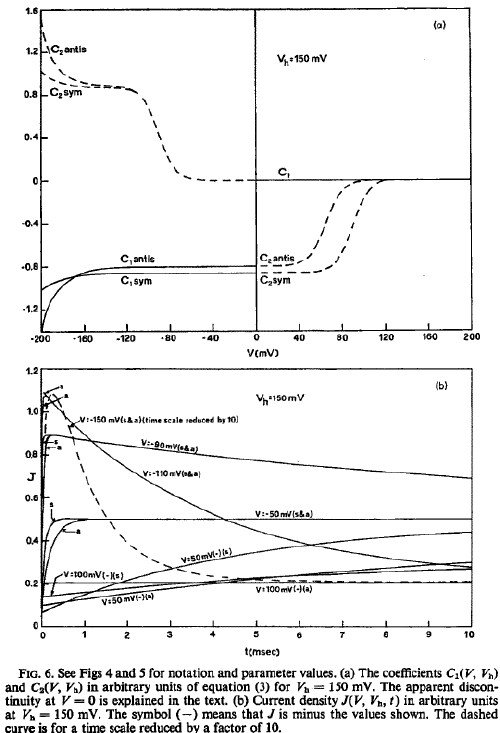
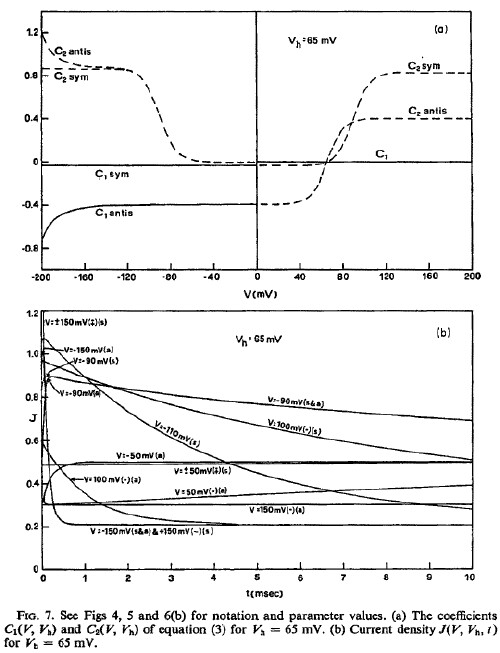
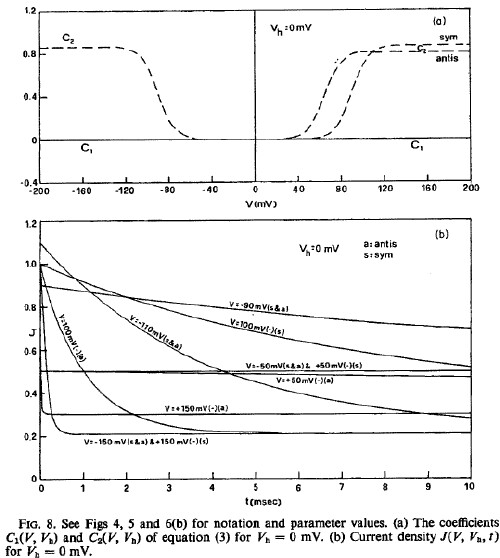
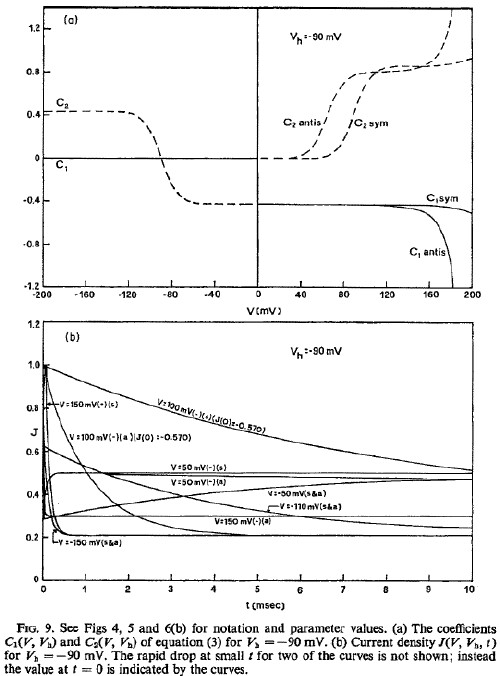
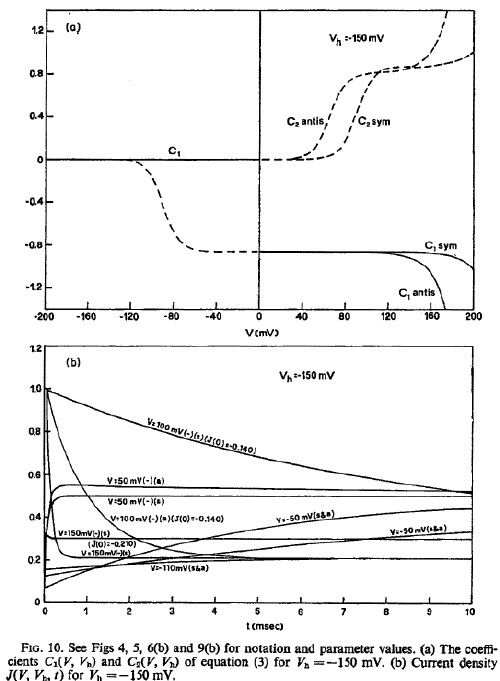
Nerve Excitation
Rationalizing the Hodgkin-Huxley Equations for Nerve Excitation
L. David Roper
http://www.roperld.com/personal/roperldavid.htm
06-Apr-2016